Un recueil d’exercices proposé par le Groupe Banqoutil donnant l’esprit de ce qui pourrait être demandé à l’examen du diplôme national du brevet, et en lien avec la tâche complexe.
- Les outils actuellement élaborés par l’équipe sont des documents de travail susceptibles d’être modifiés ou complétés.
- Chacun d’eux est composé d’un énoncé d’exercice, d’items proposés à l’évaluation avec critères de correction, et éventuellement de commentaires et d’analyses de copies d’élèves.
- L’évaluation porte sur trois items de la compétence 3.
Leur choix, arbitraire et non exhaustif, a été guidé par la présentation des évaluations de cinquième et suit l’un des schémas ci-dessous :- 2 items transversaux (« capacités ») et 1 item mathématique (« connaissances »)
- 1 item transversal (« capacités ») et 2 items mathématiques (« connaissances »).
| Capacités transversales | Connaissances mathématiques |
|---|---|
| Rechercher, extraire et organiser l’information utile | Organisation et gestion de données |
| Mesurer, calculer, appliquer des consignes | Nombres et calculs |
| Modéliser, conjecturer, raisonner et démontrer | Géométrie |
| Argumenter et présenter les résultats à l’aide d’un langage adapté | Grandeurs et mesures |
Extrait de la note de service n°2012-029 du 24 février 2012 (BOEN n°13 du 29-3-2012)
Épreuve de mathématiques
- Durée de l’épreuve : 2 heures.
- Le sujet est constitué de six à dix exercices indépendants. Les exercices correspondent aux exigences du socle commun pour la série professionnelle et portent sur différentes parties du programme de troisième pour la série générale. L’ensemble du sujet doit préserver un équilibre entre les quatre premiers items de la compétence 3 du socle commun de connaissances et de compétences - Les principaux éléments de mathématiques et la culture scientifique et technologique - appliqués à l’activité de résolution d’un problème mathématique :
- rechercher, extraire et organiser l’information utile ;
- mesurer, calculer, appliquer des consignes ;
- modéliser, conjecturer, raisonner et démontrer ;
- argumenter et présenter les résultats à l’aide d’un langage adapté.
- L’essentiel de l’épreuve évalue ces capacités.
- Un des exercices au moins a pour objet une tâche non guidée, exigeant une prise d’initiative de la part du candidat.
- Notation de l’épreuve : l’épreuve est notée sur 40 points.
- Chaque exercice est noté entre 3 et 8 points, le total étant de 36 points. La note attribuée à chaque exercice est indiquée dans le sujet. Par ailleurs, 4 points sont réservés à la maîtrise de la langue.
Exercices
(Il est aussi possible d’accéder aux fichiers sur le site du rectorat)
| LA PROMOTION DE PRINTEMPS | ||
| Pourcentages | À l’occasion de la sortie de sa collection de printemps, un magasin de vêtements propose la promotion suivante :
Anne-Marie désire acheter un pull à 21 €, une veste à 60 € et une robe à 48 €.Quel pourcentage de réduction peut-elle obtenir au maximum sur l’ensemble de ses achats ?
| |
| LE BUS DE LA RUE DE LA POMME | |||
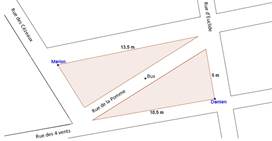
| Triangle rectangle, Pythagore | Marion et Damien doivent prendre le bus à l’arrêt situé au milieu de la rue de la Pomme.
Marion est convaincue qu’elle a un trajet moins long que Damien. Qu’en pensez-vous ? Justifiez la réponse. La rue des 4 vents est perpendiculaire à la rue d’Euclide.
| ||
| LA COMMANDE GROUPÉE | ||
| Extraire l’information, pourcentages, choix des opérations | Madame Martin, professeur de mathématiques en terminale, désire faire un achat groupé d’annales non corrigées pour les 22 élèves de sa classe.
Un éditeur lui fait l’offre ci-contre. Lorsqu’elle présente son bon de commande au libraire, il lui accorde alors une remise de 4 %. Combien chaque élève devra-t-il payer ?
|
| LE TOURNOI | ||
| PGCD, diviseurs | Le professeur d’Éducation Physique et Sportive organise en fin d’année un tournoi avec les 147 élèves de 4e et les 105 élèves de 3e. Il souhaite les répartir de telle façon que dans tous les groupes il y ait le même nombre d’élèves de 3e, et que dans tous les groupes, il y ait le même nombre d’élèves de 4e. Il souhaite également avoir le plus grand nombre possible de groupes.
Combien de groupes pourra-t-il faire et comment ces groupes seront-ils constitués ? Justifier la réponse. | |
| LES BONBONS | ||
| Probabilité, proportion, nombres, comparaison | Annie préfère les bonbons à la menthe.
Dans quel paquet lui conseillez-vous de piocher : un paquet de 100 avec 35 bonbons à la menthe, ou un paquet de 60 avec 19 bonbons à la menthe ? Justifiez la réponse. | |
| LES DÉS | ||
| Organisation et gestion de données, probabilité | Pour éviter de faire la vaisselle, Alex annonce à sa petite sœur : « C’est toi qui fais la vaisselle si je devine ce que diront les dés ! ». Sa sœur ayant accepté, il annonce : « 7 ! ».
Elle lance alors les dés et obtient le résultat ci-contre. À la place d’Alex, auriez-vous choisi le même nombre ? Justifiez la réponse. |
| LA FUITE | ||
| Proportionnalité, volume, durée, conversion | Une salle de bains est équipée d’une vasque.
Le robinet fuit à raison d’une goutte par seconde. En moyenne, 20 gouttes d’eau correspondent à un millilitre (1 mL). Le volume d’un cylindre est donné par la formule : V = pr ²h, où r désigne le rayon et h la hauteur du cylindre. Caractéristiques :
L’évacuation de la vasque étant fermée, y a-t-il un risque de débordement si le logement reste inoccupé pendant une semaine ?
|
| LES GLACES | ||
| Volume, cône, boule, conversion | Nous sommes lundi et un restaurateur reçoit 15 personnes mardi.
Il se demande : « Si tous prennent des cornets de glaces à la fraise, aurai-je assez de glace ? Dois-je faire une commande dès ce soir ? » Que doit faire le restaurateur ? Justifier la réponse. (Quatre documents sont joints). | |
| LA MAQUETTE | ||
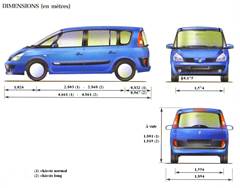
| Recherche d’information, échelle, comparaison de nombres décimaux, conversion | Le constructeur RENAULT donne pour le véhicule automobile ESPACE IV les dimensions ci-contre.
Dans une brocante, Xavier trouve la réplique exacte à l’échelle 1/20e de sa voiture, un véhicule RENAULT ESPACE IV (châssis normal). Il a chez lui une boîte parallélépipédique en verre dont les dimensions intérieures sont : longueur L = 23,5 cm, largeur l = 9,4 cm et hauteur h = 9,1 cm. Cette boîte est-elle assez grande pour pouvoir y exposer la maquette ? Justifier la réponse. |
| LE RALLYE MATH | ||
| Probabilité, proportion, nombres, comparaison | Deux classes de troisième ont gagné un prix au dernier rallye mathématique.
Un élève de chaque classe sera tiré au sort pour recevoir le prix. Il y a 11 filles et 14 garçons en 3e A et 13 filles et 16 garçons en 3e B. Dans quelle classe a-t-on le plus de chances que ce soit une fille qui représente ses camarades ? Justifier la réponse. | |
| LE BLOUSON | ||
| Pourcentage, comparaison de nombres décimaux | Un blouson soldé bénéficie d’une réduction de 40% dans le magasin « sportwear ». Son prix de départ est de 94 euros.
Le même blouson à 94 euros subit dans le magasin « tendance » deux baisses successives : une première remise de 10%, puis une deuxième de 30%. Où iriez-vous acheter votre blouson :
Justifiez la réponse. | |
| LES CARTOUCHES D’ENCRE | ||
| Modélisation, essai-erreur, fonction linéaire, fonction affine, inéquation | À partir de combien de cartouches le prix sur l’Internet est-il plus intéressant que celui en magasin ?
Justifier la réponse. |
| LE COCKTAIL | ||
| Fraction, conversion | Les 29 élèves de la classe de Léa comptent préparer, à l’occasion du départ en retraite de leur professeur de mathématiques, le fameux cocktail pétillant dont voici la recette :
Un tiers de jus d’orange, un quart de jus de mangue, un sixième de jus de goyave. Compléter avec de la limonade. Léa propose de fournir la limonade et d’en apporter une bouteille de 1,5 L.
| |
| LA MASSE ET LE POIDS | ||
| Recherche d’information, lecture de tableau, proportionnalité, équation | La masse et le poids sont des grandeurs différentes. Elles sont reliées l’une à l’autre par la relation :
Les informations fournies dans ces documents […] permettent-elles de déterminer le poids sur la Terre de Neil Armstrong équipé de sa combinaison ? Justifier la réponse. | |
| LE MOULIN | ||
| Proportionnalité, conversion, puissance de 10 | Un moulin produit 7,5 m3 de farine par semaine. Il produit la même quantité de farine chaque jour travaillé. La farine est entreposée dans des sacs de 50 kg. Un centimètre cube de farine pèse 0,0008 kg.
Combien de sacs faut-il prévoir pour une journée de travail ? Justifier la réponse. | |
| PARIS-MARSEILLE | ||
| Recherche d’information, proportionnalité, durée | Joffrey doit effectuer un trajet Paris (75000) – Marseille (13000), il hésite entre deux options : par autoroute et hors autoroute.
Il utilise un véhicule diesel. Le prix d’un litre de carburant est de 1,33 euro. Consommation de son véhicule pour 100 km :
Joffrey dispose de 120 euros pour ses frais de transports. Quel trajet lui conseilleriez-vous de choisir ?
|
| SOMMES D’ENTIERS CONSÉCUTIFS | ||
| Calcul numérique, contre-exemple | Xavier constate que pour calculer 9 + 10 + 11 + 12, il est possible de simplifier le calcul en remplaçant cette somme par celle obtenue en continuant la liste des nombres mais avec un terme de moins.
En effet 9 + 10 + 11 + 12 = 13 + 14 + 15. On a bien simplifié le calcul puisque l’on est passé de 4 termes donc 3 additions à 3 termes donc 2 additions. Xavier choisit un autre exemple et constate également que : 16 +17 + 18 + 19 + 20 = 21 + 22 + 23 + 24. On passe ici de 4 additions à seulement 3. Peut-on appliquer cette méthode de simplification au calcul des sommes suivantes : 4 + 5 + 6 25 + 26 + 27 + 28 + 29 + 30 36 + 37 + 38 + 39 + 40 + 41 + 42 ? Cette affirmation est-elle toujours vraie ? Justifier la réponse. | |
| À LA TERRASSE D’UN CAFÉ | ||
| Équation, système d’équations, essai-erreur, méthodes arithmétiques | Version 1
À la terrasse d’un café, le serveur annonce : « 2 thés et 3 sodas ; cela fera 12,20 euros s’il vous plaît ! ».
Version 2
| |